UTN-GFA.github.io

Dimensiones, filtros y operaciones de la Redes Neuronales Convolucionales
1. Objetivo
Comprender cómo operan los distintos componentes y procesos de una red neuronal convolucional tales como su arquitectura, dimensión de filtros, operaciones aritméticas, conformación de los mapas de características (features maps) y los vínculos entre las diferentes capas. Para, de esta manera, poder diseñar y utilizarlas para procesar una imágen y detectar características de la misma con mayor conocimiento.
2. Introducción
Para poder entender las características de una red neuronal convolucional (CNN) resulta una buena idea comenzar por entender cómo operan sus componentes de forma simplificada para luego extrapolar este comportamiento al resto de la estructura.
En este documento nos centraremos en la arquitectura de la Cifar-10 CNN provista por Jason Brownlee en su blog Machine Learning Mastery para poder llevar los conceptos teóricos a ejemplos prácticos que resulten fácilmente extrapolables a otros tipos de arquitecturas neuronales.
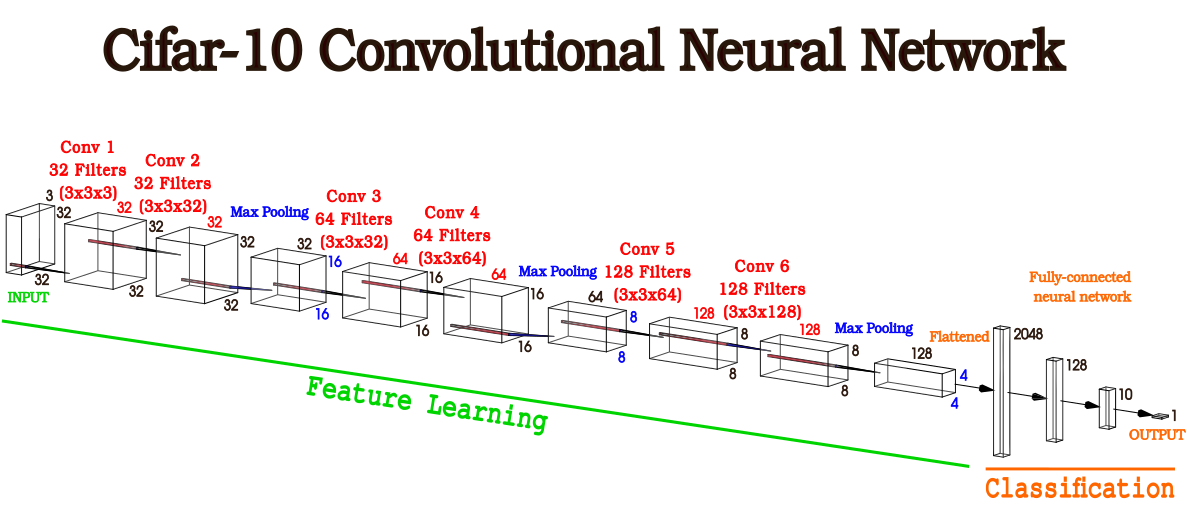 Figura 1 - Arquitectura Cifar-10 donde se evidencian las diferentes capas con las dimensiones de sus componentes
Figura 1 - Arquitectura Cifar-10 donde se evidencian las diferentes capas con las dimensiones de sus componentes
3. Tamaño de los filtros y mapas de características
La principal operación que realiza una red neuronal convolucional es la convolución. Esta operación es la que da origen a los llamados mapas de características, es decir, a un conjunto de píxeles que guarda una relación con la imagen de entrada.
La convolución se realiza en principio con la imagen que recibe la CNN y el primer filtro para dar como resultado un mapa de características que tendrá las siguientes dimensiones (figura 2):
Alto y largo: Igual a la de la imagen de entrada (INPUT) Profundidad (Cantidad de canales): Será igual a la cantidad de filtros que integren cada capa de convolución.
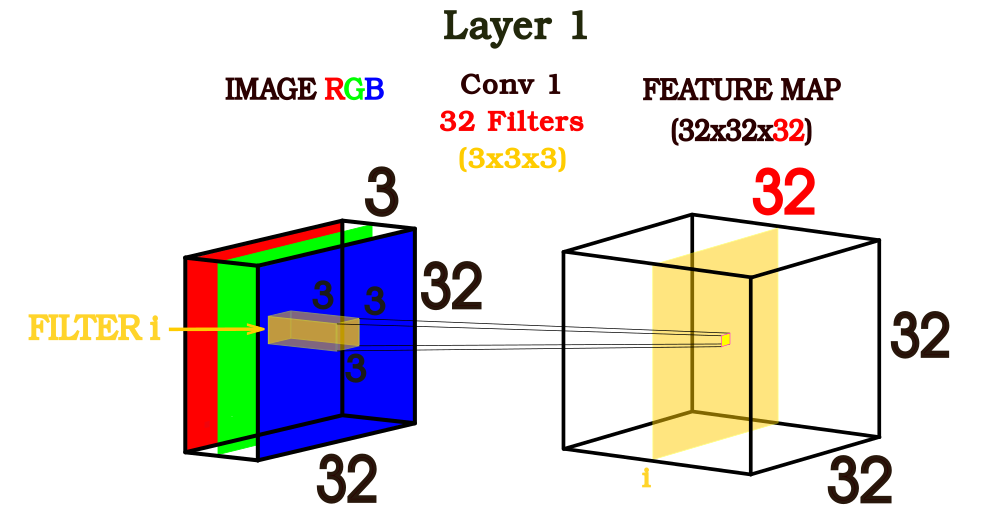 Figura 2
Figura 2
Luego de creado el primer mapa de característica, la red neuronal convolucional procede a crear más mapas de características, tantos como capas tenga la arquitectura de la red.
Si analizamos la cuarta capa dentro de la arquitectura propuesta podemos observar que se realizan operaciones de convolución entre un mapa de características y 64 filtros dando como resultado otro mapa de características con una profundidad de 64. Por lo tanto, la profundidad del mapa de características va a quedar determinada por la cantidad de filtros propuestos por la arquitectura de esa capa.
Como se observa en la figura 3, si convolucionamos el mapa de características de la capa 4 con el filtro “k” en una determinada posición (h, w) se obtiene un pixel que integrará el canal “k” en otro mapa de características. Los píxeles restantes del canal “k” del feature map serán resultado de desplazar el filtro “k” por el resto del feature map de la capa anterior. Los restantes canales del segundo mapa de características serán resultado de convolucionar y desplazar los restantes filtros de la capa 4 de la red.
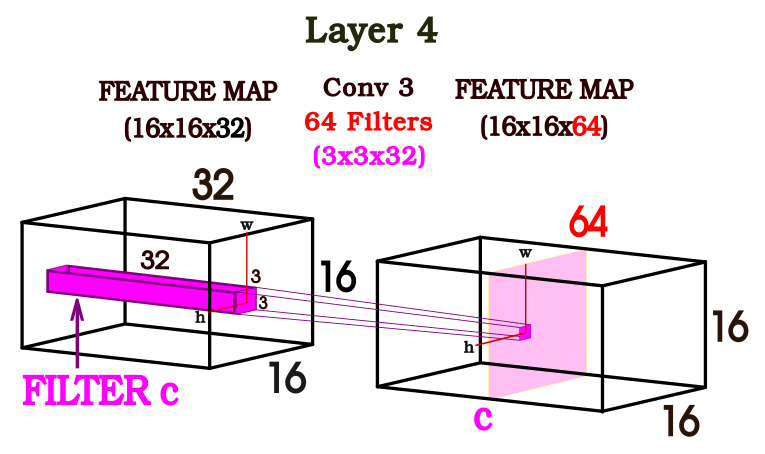 Figura 3
Figura 3
Resulta interesante que a medida que hay más operaciones de convolución la red neuronal es capaz de detectar más características de la imagen que se busca analizar. Las primeras capas de la red detectan líneas, curvas y a medida que agregamos más capas se podrán identificar formas cada vez más complejas. Esto dependerá del problema que queramos abordar, no es lo mismo clasificar imágenes de ratones y elefantes que clasificar imágenes de personas por su rango etario.
Cantidad de parámetros a entrenar
Primero veamos cómo se calcula la cantidad de parámetros a aprender en cada tipo de capa y luego calculemos la cantidad de parámetros en nuestro ejemplo.
Para conocer cuántos serán los parámetros a calcular en cada capa de la red convolucional solo basta con multiplicar las dimensiones de un filtro, sumarle 1 por la neurona Bias (se agrega por salida en una conexión entre 2 capas) por la cantidad total de filtros presentes en una capa.
En nuestro caso tenemos 12 capas:
- Conv2d: 32 Filtros de 3x3x3, por lo tanto se calcularán (3x3x3+1)x32 = 896 parámetros.
- Conv2d_1: 32 Filtros de 3x3x32, (3x3x32+1)x32 = 9248 parámetros.
- Max_pooling2d: No se calculan parámetros.
- Conv2d_2: 64 Filtros de 3x3x32, (3x3x32+1)x64 = 18496 parámetros.
- Conv2d_3:64 Filtros de 3x3x64, (3x3x64+1)x64 = 36928 parámetros.
- Max_pooling2d_1: No se calculan parámetros..
- Conv2d_4: 128 Filtros de 3x3x64, (3x3x64+1)x128 = 73856 parámetros.
- Conv2d_5: 128 FIltros de 3x3x128, (3x3x128+1)x128 = 147584 parámetros.
- Max_pooling2d_2: No se calculan parámetros.
- Flatten: No se calculan parámetros.
- Dense: (2048+1)x128 = 262272 parámetros.
- Desnse_1: (128+1)x10 = 1290 parámetros.
Para calcular la cantidad de parámetros de las capas de la Fully-Connected Neural Network solo debemos multiplicar la cantidad de neuronas de la capa anterior sumado 1 (bias) a la cantidad de neuronas de la capa densa.
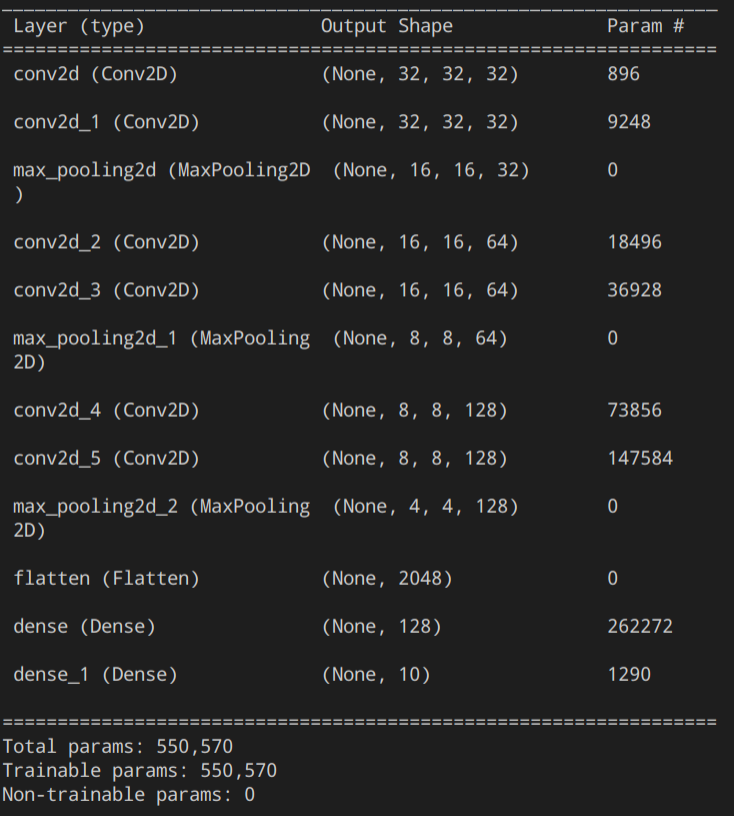
Para poder conocer la cantidad de parametros por capa de la red neuronal, podemos llamar a la función summary() dentro de nuestro código para conocer el resto de parámetros.
El siguiente diagrama muestra la salida de la función summary():
5. Operación entre los filtros, la imágen y los mapas de características
Para entender cómo operan las redes convolucionales analizaremos la figura 4 enfocada en la primera capa de la CNN. Los cuadrados rojo, verde y azul representan una submatriz de 3x3 de cada uno de los canales de la imágen de entrada de la red neural convolucional (Imagen RGB). Los cuadrados amarillos representan cada kernel del primer filtro de la primer capa de la red. Cada uno de los valores de la imagen se multiplican uno a uno con los valores de los kernels, es decir, los valores de la submatriz roja se multiplican con los valores del primer kernel y el resultado se suma a la multiplicación entre los valores de la submatriz verde con el segundo kernel del filtro y a su vez este resultado se suma a la multiplicación de los valores de la submatriz azul con los valores del tercer kernel. Luego, se evalúa el resultado en una función de activación (en este ejemplo: RELU) para finalmente sumarle un bias. Por cada filtro que se le aplica a la imagen el bias tomará un valor distinto.
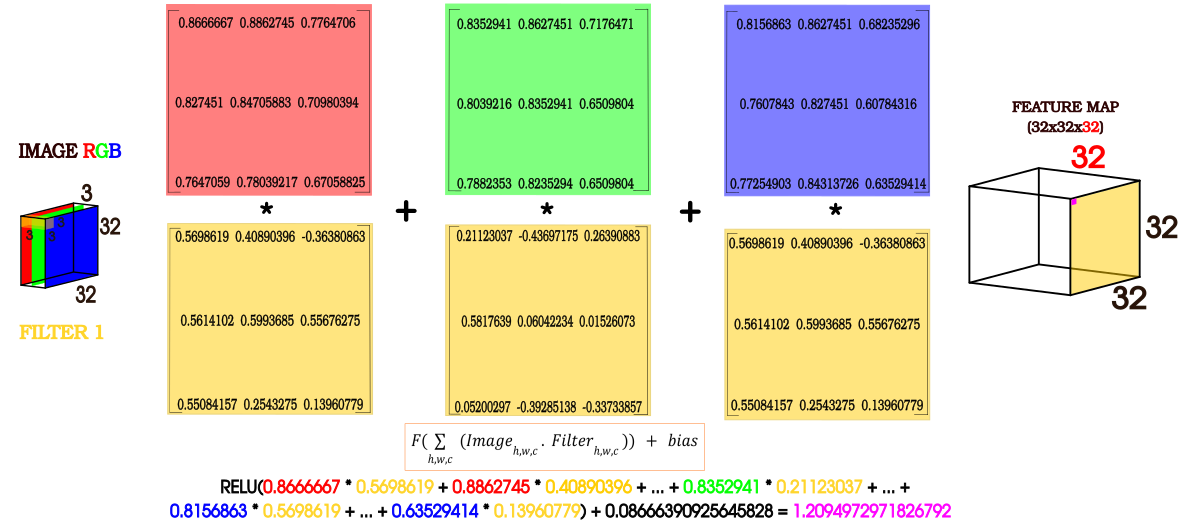 Figura 4
Figura 4
Los valores de los filtros varían entre -1 y 1, mientras que los valores de la imagen de entrada y los feature maps de la red entre 0 y 1.
6. Visualización de Mapas de Características
Para poder ganar cierta intuición al momento de trabajar con redes neuronales además de adentrarnos en las características cuantitativas de la CNN, podemos ver qué cualidades posee. En la figura 5 se puede observar 4 capas que integran a cada uno de los mapas de características de la red neuronal convolucional. Se incluyeron 4 a modo de simplificación, pero la cantidad de capas de cada mapa de característica (número de canales) corresponde a la cantidad de filtros que se aplique por capa.

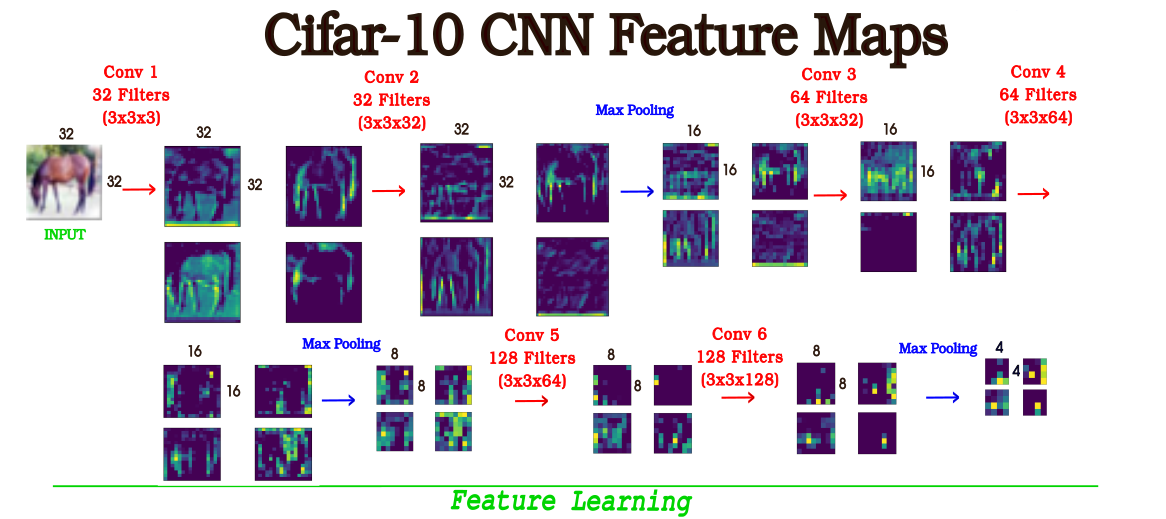
7. Recursos
Dentro del repositorio se encuentra:
- Cifar-10-CNN.py
- Final_model.h5: CNN ya entrenada.
- Horse5.png: IMAGE Input.
- Prediction_cnn.py: Programa que permite clasificar imágenes de la CNN Cifar-10.
- Operation_validation.py: Programa para validar el cálculo que realiza internamente la red neuronal.
- Visualize_feature_prediction.py: Programa que permite visualizar los mapas de características de toda la red neuronal.
8. Fuentes
Tutorial — How to visualize Feature Maps directly from CNN layers
Convolutional Neural Network: Feature Map and Filter Visualization
How to Visualize Filters and Feature Maps in Convolutional Neural Networks
Deep Learning in the Trenches: Understanding Inception Network from Scratch